Gravitational Interaction of Vibrating Systems
J. Dual, B. Zybach, S. Blunier, T. Brack, J. Fankhauser, S. Kaufmann, F. Palmegiano, D. Scheiwiller, J.C. Tomasina, F. Balabdaoui
Theory and Measurement of Gravity
Nowadays, gravity is most accurately described by Einstein’s general theory of relativity. However, in the laboratory, gravity is well approximated by Newton’s law of universal gravitation from 1687, stating that every point mass m1 attracts every other point mass m2 by a force
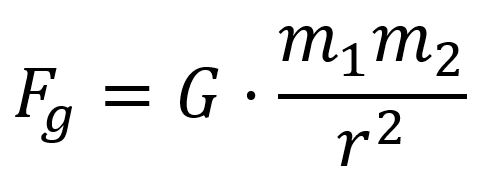
.
acting along the line connecting the two points, where 𝑟 is the distance between the point masses and 𝐺 is the Newtonian constant of gravitation [5]
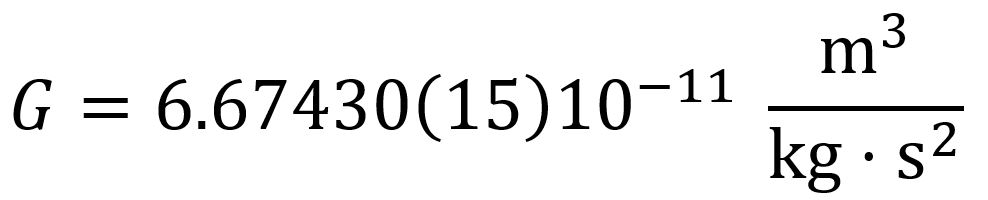
.
In order to determine 𝐺, Henry Cavendish established in 1798 the measuring principle of a static torsion balance [2], which is still used today in improved versions. Since then, only few other principles have been used, such as free fall or dynamic experiments (vibrating or rotating rods). Due to the relatively large uncertainties in the measurements and/or theory, the natural constant 𝐺 is the least known of all the basic constants of physics, cf. Fig. 2
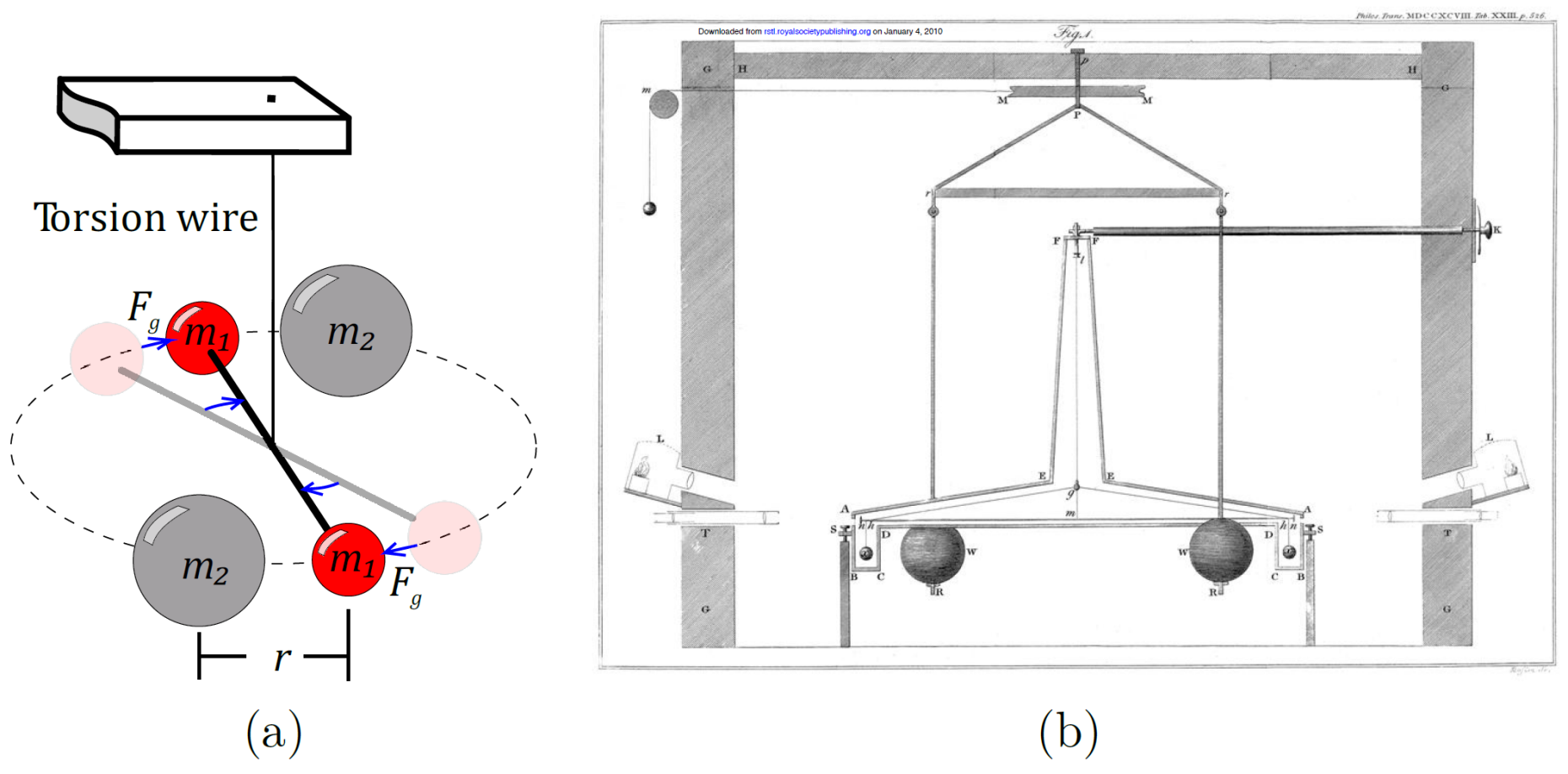
Figure 1: Torsion balance to measure the attraction of two masses due to gravitation. (a) Measurement scheme; (b) Drawing of the first setup by Cavendish in 1798. Extract from [2]
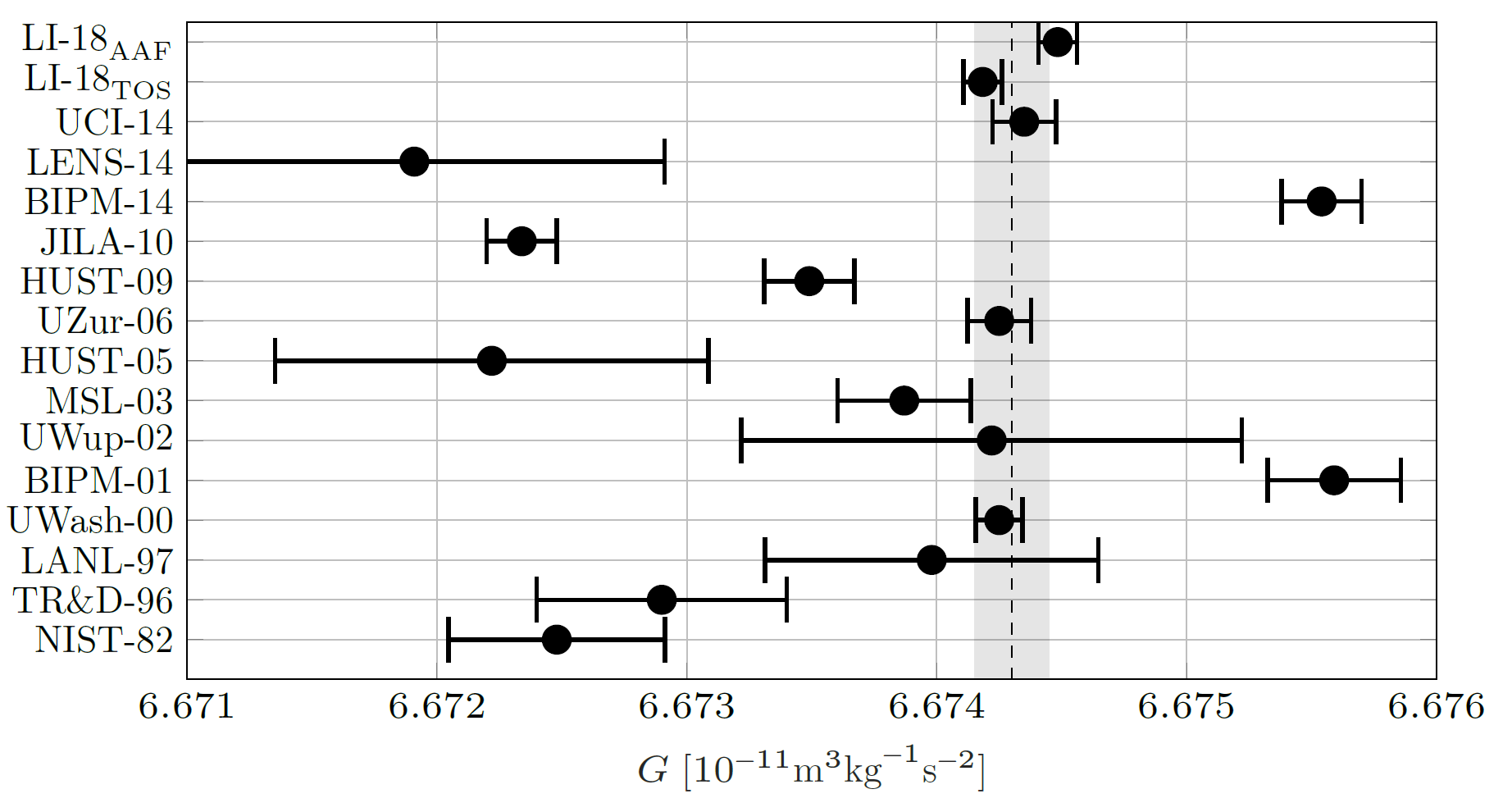
Figure 2: Measurements of 𝐺 taken over the past 40 years. The dashed line denotes the 2018 CODATA recommended value. The uncertainties are indicated by error bars and the shaded area. Data from [3] and [4].
In contrast to Newton, Einstein predicts the existence of gravitational waves propagating from their source at the speed of light. Such waves could be first detected in 2015 by the LIGO (Laser Interferometer Gravitational-Wave Observatory) [1].

Figure 3: Simplified diagram of an Advanced LIGO detector (not to scale) and measured signal of the gravitational event GW150914 observed by the LIGO Hanford, Washington. Figures from [1].
Goal and Measurement Method
Goal
Establish a new high precision experiment to investigate various aspects of
gravity, such as
- the value of the gravitational constant 𝐺
- the inverse square law 𝐹𝑔 ∼ 𝑟2
- gravitational shielding
Measurement Methods
The experiment is dynamic, thereby eliminating gravitational influences from the environment. It consists of a detector beam and a mechanically decoupled transmitter.
The transmitter is excited externally in order to produce a vibration of large amplitude, with a frequency as close to the first bending resonance frequency of the detector beam as possible (ca. 42 Hz). With proper decoupling, the detector beam will experience gravitational forces only. Due to the dynamic movement of the transmitter and hence a dynamic gravitational force, a first mode bending vibration of the detector beam is excited.
Due to resonance and the resulting amplification (Q ∼ 15000), measurable vibrations develop. The detector deflection is measured using multiple laser vibrometers and high precision lock-in amplifiers. The amplitudes are then linked to the excitation force using models from continuum mechanics.

Figure 4: Measurement principle: while the transmitter is excited externally, the detector beam performs gravitation induced vibrations that can be detected optically.
Challenges
- eliminate parasitic coupling (mechanic, acoustic, electromagnetic, etc.)
- measurement of extremely small movements (10-11 m/s; 10-13 m)
- ensure stable environmental conditions (𝛥𝑇 ∼ 10−3 °C/h, pressure, etc.)